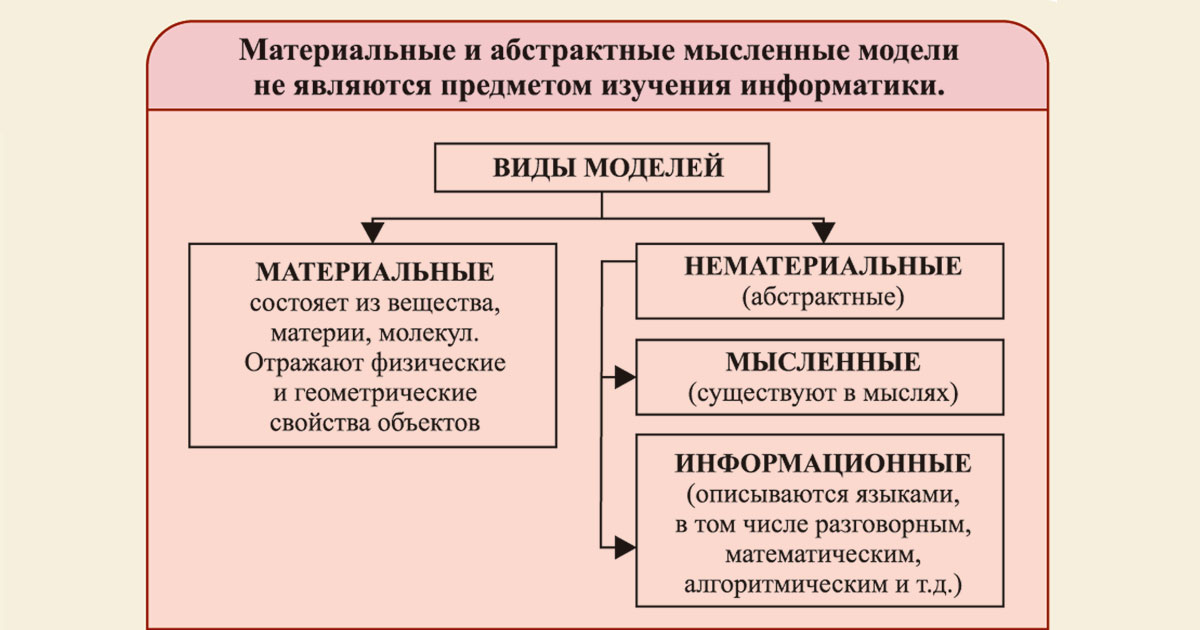
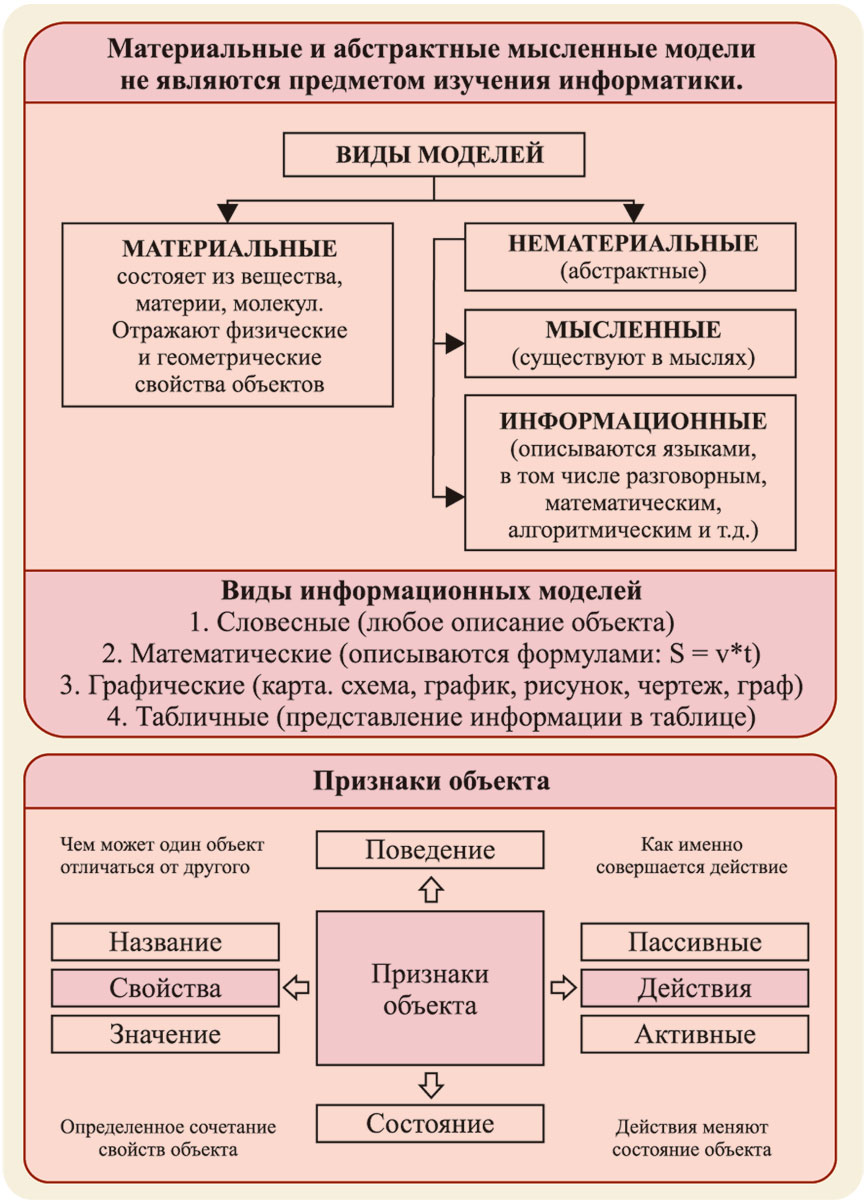
Моделирование – это замена реального объекта, процесса, явления его подходящей копией, которая проще изучаемого оригинала, но сохраняет и отражает его существенные особенности и может помочь в изучении оригинала
Объект – это некоторая часть окружающего мира, воспринимаемая человеком как единое целое.
Модель – это упрощенное подобие реального объекта, отражающее лишь некоторые (существенные свойства объекта).
Граф – это конечное множество точек, некоторые из которых соединены точками. Точки называются вершинами графа, а соединяющие их линии – ребрами (каждое ребро соединяет ровно две вершины).
Основные свойства моделей:
– адекватность;
– подробность;
– ценность.
Этапы моделирования:
1) описание цели и задач;
2) разработка информационной модели (дизайн и описание);
3) компьютерная модель (создание, тестирование);
4) исследование модели (эксперимент);
5) анализ результатов (выводы).
МОДЕЛИ И МОДЕЛИРОВАНИЕ
Алгоритм построения графа
1) Поставить точки по количеству вершин (количество строк в таблице);
2) соединять нужные вершины линиями, подписывая числа-значения из таблицы;
3) Проверить все ли данные отражены (количество линий) = 1/2 количества чисел в таблице.
ЗНАЕТЕ ЛИ ВЫ…?
Граф является графической информационной моделью, при помощи которой можно наглядно отображать взаимосвязи между объектами. Например, в виде графа можно представить дружеские отношения в классе, обозначив за вершины имена учеников, а за рёбра – наличие дружеских отношений между ними.
Из данного примера понятно, что в графе из одной вершины может исходить любое количество рёбер, а также могут присутствовать изолированные вершины (точки, не соединённые ни с одной другой вершиной). Рёбра графа не обязательно должны быть представлены в виде прямых линий. Точки, обозначающие вершины графа, можно расставлять на плоскости произвольно.
Основы теории графов как математической науки заложил в 1736 г. Леонард Эйлер, рассматривая задачу о кенигсбергских мостах. Задача о семи кёнигсбергских мостах – старинная математическая задача, в которой спрашивалось, как можно пройти по всем семи мостам Кёнигсберга, не проходя ни по одному из них дважды. Была решена в 1736 году Леонардом Эйлером, доказавшим, что это невозможно, и изобретшим таким образом эйлеровы циклы. Сегодня эта задача стала классической.
Все самое актуальное, важное и интересное - в Телеграм-канале «Немцы Казахстана». Будь в курсе событий! https://t.me/daz_asia
